Porporció Àuria

La natura és una font de bellesa inesgotable, si l’observes amb deteniment pots trobar relacions entre formes i grandàries que mantenen una certa proporció. Aquesta proporció s’anomena “Proporció àuria” o “Divina proporció”.

Hi ha constància de que ja els grecs la coneixien, per aquest motiu es simbolitza amb la lletra grega “phi” en honor a l’escultor grec Fidias.

És molt curiós com formes que guarden aquesta proporció
son agradables a la vista

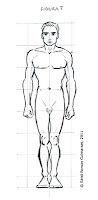
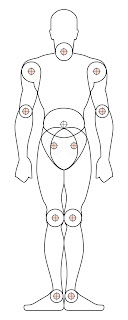
A la natura hi han molts exemples, com la disposició de les llavors de la flor del girasol, l’espiral de la closa d’un caragol, la posició dels pètals d’una rosa, el propi cos humà, o fins i tot els braços de la nostra galàxia (la Via Làctia).

Però no només es troba a la natura, algunes figures geomètriques mantenen aquesta proporció, i l’home l’ha utilitzat en tots els camps de les arts (arquitectura, pintura, escultura, fotografia, música, etc.). La trobaràs en objectes tan quotidians com una targeta de crèdit,, alguns envasos com els paquets de tabac, o en el disseny gràfic de logotips (pots consultar aquest enllaç on hi han interessants exemples).

La “Proporció àuria” es basa en la relació o proporció entre dos elements: Si parteixes d’una recta imaginària “AB”, i busques un punt “C” que divideixi la recta en dos segments més petits, la relació entre tota la recta “AB” amb el segment llarg “AC” ha de ser igual a la relació que hi ha entre el segment llarg “AC” i el segment curt “CB”.

  

Així tens la següent fórmula: AB/AC=AC/CB= “phi”

que et dona el valor numèric de “phi” (un número molt llarg...)

“phi”=1,618033988749894848204586834365638117720309...

Sense voler entrar molt en temes matemàtics, es tracta d’un número irracional (no vol dir que estigui boig..., vol dir que és un decimal infinit no periòdic (els decimal segueixen fins a l’infinit sense repetir-se).

Al principi treballar amb la Proporció àuria sembla complicat, però és una eina força útil en el camp del disseny gràfic i la il·lustració per crear composicions estètiques i visualment agradables. La figura més senzilla és el rectangle auri, el pots fer sense prendre mides a partir d’un quadrat. Des del punt mig de la base traça un arc que passi per una de les arestes superiors. Prolonga la base del quadrat i ja tens un rectangle auri!

També el pots fer amb una senzilla multiplicació, el costat llarg del rectangle serà igual al costat curt multiplicat per 1,618.

Ara que saps fer un rectangle auri, també saps fer una espiral àuria (ja que es pot construir a partir d’un rectangle auri). Com veus a la imatge, només has d’anar restant quadrats al rectangle auri ABCD, així aniràs obtenint nous rectangles auris més petits. En cada un dels quadrats, realitza un quadrant de circumferència amb radi igual al costat del quadrat, i centre en el vèrtex de cada un d’ells (punts 1, 2 ,3, 4, 5...), i ja tens una espectacular espiral àuria (espiral logarítmica).

 

La forma de construir una espiral àuria amaga un secret, si traces la diagonal en cada un dels rectangles auris que has creat, veuràs que totes es creuen en un punt O (quatre possibilitats), que és a la vegada el centre de l’espiral. Una espècie de forat negre o punt d’atracció visual on convergeixen tots els rectangles auris. Per aquest motiu aquest punt s’anomena “Ull de Déu”. Molt utilitzat per il·lustradors, dibuixants de còmic, i publicitaris per col·locar el que es vol destacar.

 

El Pentàgon regular, és una mica més complicat de construir però aquí tens un parell de sistemes:

1.- Pentàgon inscrit en un cercle:

 

Fes un cercle amb un compàs, a la mida que vulguis. Traça un radi qualsevol. Amb un transportador d’angles, marca 72º a partir del radi marcat (360º dividit entre cinc dona 72º, que és la mida dels angles interiors dels cinc triangles que formen el pentàgon). Pots seguir marcant cada 72º o si ho prefereixes amb un compàs transportar la mida fins tenir marcats cinc punts en la circumferència. Ara només has d’unir-los i ja tindràs el teu pentàgon regular.

2.- Pentàgon coneixent el costat:

 

Tens el segment AB que serà un dels costats del pentàgon. A partir d’un extrem, per exemple B, traça la perpendicular i transporta la mida AB per obtenir el punt G. Amb un compàs amb centre en el punt mig entre A i B (F) i radi FG, traça un arc per obtenir el punt H (on creua amb la prolongació del segment AB). Ara amb radi AH traça dos arcs amb centre en A i en B (on es creuen serà el punt D). Amb centre en D i radi AB, traça un altre arc per obtenir els punts C i E. Finalment només has d’unir els punts ABCDE i ja tens el teu pentàgon regular.

El Pentàgon regular és potser la figura àuria més perfecte. Si traces totes les seves diagonals veuràs com es crea una fantàstica estrella de cinc puntes que a la vegada te un altre pentàgon regular en el seu interior. També pots comprovar com els triangles que es creen en el interior son també triangles auris.

Amb totes aquestes formes geomètriques, tens molt camp per jugar i experimentar

El compàs auri

Una eina senzilla de construir és el Compàs auri. Permet crear relacions amb proporció àuria o comprovar si un disseny guarda entre si aquesta proporció. Per construir-lo segueix els següents passos:

1.- Talla dues tires de cartró, plàstic o fusta, de 34 cm de llarg i 2 cm d’ample.

2.- Fes els finals de les tires acabats en punta.

3.- Realitza un forat en cada tira, a 13 cm d’un dels extrems.

4.- Amb una xinxeta enquadernadora (petita peça semblant a una xinxeta però amb dues potes planes) uneix les dues tires de manera que es puguin articular.

Ja has construït el teu Compàs auri, la relació entre les distàncies de les puntes dels dos costats és “phi”.
Amb el compàs auri, els nens es poden divertir fent de detectius per la casa a la cerca d'objectes que tinguin proporcions àuries.

A partir d’ara et convido a incorporar la Proporció àuria en els teus dibuixos i creacions!